PPO
PPO与TRPO旨在解决相同的问题:在策略梯度定理的步长$\alpha$的选取中,如何选取合适的步长,使得更新的参数尽可能对应最好的策略,但也不至于走得太远,以至于导致性能崩溃。
PPO也继承了TRPO的核心思想:引入**重要性采样,提高样本效率**;同时,通过某种方式来约束新旧策略间的差异不要太大。
不同的是,TRPO 试图用复杂的二阶方法解决这个问题(对目标函数采取一阶近似,约束条件采取二阶近似),然而PPO采用了一系列的一阶方法(Clip),它们使用一些其他技巧来使新策略接近旧策略。PPO在算法上更加简单,且效果不输于TRPO算法的效果。
回顾一下,TRPO算法对以下目标函数进行优化问题的求解:
$$\underset{\theta}{\operatorname{maximize}} \hat {\mathbb{E}}_{t}\left[\frac{\pi\_\theta(a_t \mid s_t)}{\pi_{\theta_{old}}(a_t \mid s_t)} A_{t} \right] \ \text { subject to } \hat {\mathbb{E}}_{t}\left[{\mathrm{KL}}\left(\pi_{\theta_{\text {old }}}(\cdot \mid s) | \pi_\theta(\cdot \mid s)\right)\right] \leq \delta\tag{1} $$
这里,$\theta_{old}$是更新之前的策略参数向量,$A_t$是在时刻$t$的优势函数估计,期望$\hat {\mathbb E}_t$是在采样和优化之间交替的算法中,有限批次样本的经验平均值。求解的过程采用到了共轭梯度和线性搜索的方式。TRPO在目标函数中,另外增加了一个约束条件。在推导该式的过程中, 涉及到了一个将KL散度****作为惩罚项的极值问题,转化为KL散度作为约束条件的优化问题的过程。将KL散度作为惩罚项的问题,公式如下:
$$\theta_{new}=\arg \max_\theta\left[L_{\theta_{\text {old }}}(\theta)-C D_{K L}^{\max }\left(\theta_{\text {old }}, \theta\right)\right]\tag{TRPO-12} $$
然而,因为权重难以选择和调整的问题,因此TRPO并没有采取这样的方式进行目标函数的设定。
PPO-惩罚(PPO1)
PPO-惩罚(PPO1)用拉格朗日乘数法直接将KL散度的限制放入了目标函数,因此变成了一个无约束的优化问题,在迭代的过程中不断更新KL散度前的系数。这里,使用几个阶段的小批量SGD,优化KL惩罚目标,其更新方式即为公式(2)
$$\underset{\theta}{\operatorname{maximize}} \hat{\mathbb{E}}_t\left[\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)} \hat{A}_t-\beta \mathrm{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right]\tag{2} $$
为了对$\beta$进行动态调整,作者提出了自适应KL散度(adaptive KL divergence)的思想。具体做法是,在每个epoch对KL惩罚目标进行优化后,计算$d=\hat{\mathbb{E}}_t\left[\mathrm{KL}\left[\pi_{\theta_{\text {old }}}\left(\cdot \mid s_t\right), \pi_\theta\left(\cdot \mid s_t\right)\right]\right]$:
- 如果$d<\frac{\delta}{1.5}$,则$\beta \leftarrow \frac{\beta}{2}$。
- 如果$d>1.5 \delta$,则$\beta \leftarrow 2{\beta}$
- 否则,$\beta$保持不变。
在这里,更新的$\beta$用于下一次迭代时的参数更新。
PPO这里使用了GAE进行计算
PPO-截断(PPO2)
PPO2在限制新的策略参数与旧的策略参数的距离上,相比于PPO1更加直接。区别于PPO1使用KL散度的方式进行限制,PPO2直接在目标函数上进行限制:
$$L^{C L I P}(\theta)=\hat{\mathbb{E}}_t\left[\min \left(r_t(\theta) \hat{A}_t, \operatorname{clip}\left(r_t(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_t\right)\right]\tag{3} $$
其中,
- $r_t(\theta)=\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)}$ 称为概率比,易得$r_t(\theta_{old})=1$
- $\operatorname{clip}\left(r_t(\theta), 1-\epsilon, 1+\epsilon\right)$指的是将$r_t(\theta)$限制在$[1-\epsilon,1+\epsilon]$的范围内。
- $clip(x,l,r):=max(min(x,r),l)$即把$x$限制在$[l,r]$内
- $\epsilon$为超参数,表示进行截断操作的范围,一般取$\epsilon=0.2$。
这样,就始终保证了新旧策略的比值在$[1-\epsilon,1+\epsilon]$的范围内,保证了两个策略的差距不会太大。
PPO2中,较为精妙的一点是在$\text{clip}$操作后乘了$\hat A_i$(以下用$A$表示),而优势函数$A$是有正负的。
如下面两张图所示
$\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{old}}\left(a_t \mid s_t\right)}$ 是绿色的线;
$\operatorname{clip}\left(\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{old}}\left(a_t \mid s_t\right)}, 1-\varepsilon, 1+\varepsilon\right)=max[min(r_t(\theta),1+\epsilon),1-\epsilon]]$ 是红色的线;
在绿色的线与红色的线中间,我们要取一个最小的结果。
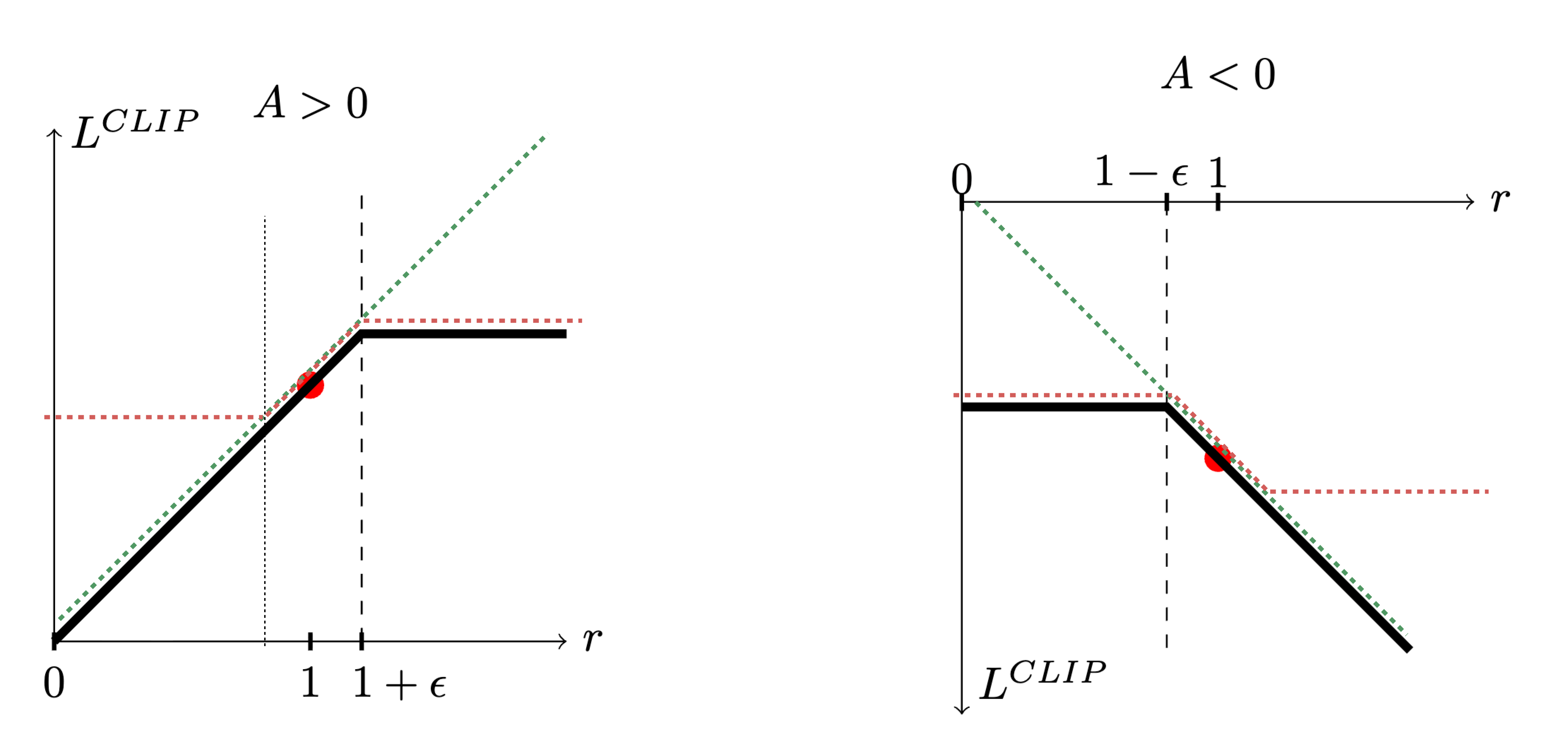
如图所示,假设前面乘上的项 $A>0$ ,取最小的结果,就是黑色色的这条线。如右图所示,如果 $A<0$ 0,取最小结果的以后,就得到红色的这条线。
下面来做一个详细的讨论。
- 如果 $A>0$,也就是某一个状态-动作二元组相比于状态价值函数$V$更好,我们就希望增大这个状态-动作二元组的概率。也就是,我们想让 $\pi_\theta\left(a_t \mid s_t\right)$ 越大越好,但它与 $\pi_{\theta_{\text {old }}}\left(a_t \mid s_t\right)$ 的比值不可以超过 $1+\epsilon$ 。如果超过 $1+\epsilon$,新策略与旧策略之间的差距就会过大而产生问题。所以在训练的时候,当 $\pi_\theta\left(a_t \mid s_t\right)$ 被训练到$\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{old}}\left(a_t \mid s_t\right)}>1+\epsilon$时,训练就会停止。
- 如果 $A<0$,也就是某一个状态-动作二元组相比于状态价值函数$V$更差,那么我们希望把 $\pi_\theta\left(a_t \mid s_t\right)$ 减小。如果 $\pi_\theta\left(a_t \mid s_t\right)$ 比 $\pi_{\theta_{old}}\left(a_t \mid s_t\right)$ 还大,那我们就尽量把它减小,减到 $\frac{\pi_\theta\left(a_t \mid s_t\right)}{\pi_{\theta_{old}}\left(a_t \mid s_t\right)}$ 是 $1-\epsilon$ 的时候停止, 此时不用再减得更小,即新旧策略之间的差距不会过大。