DeepSeek

本文为DeepSeek系列论文阅读, 包含

• Deepseek Math
• DeepSeek R1

DeepSeek Math

RL Part – GRPO

Group Relative Policy Optimization

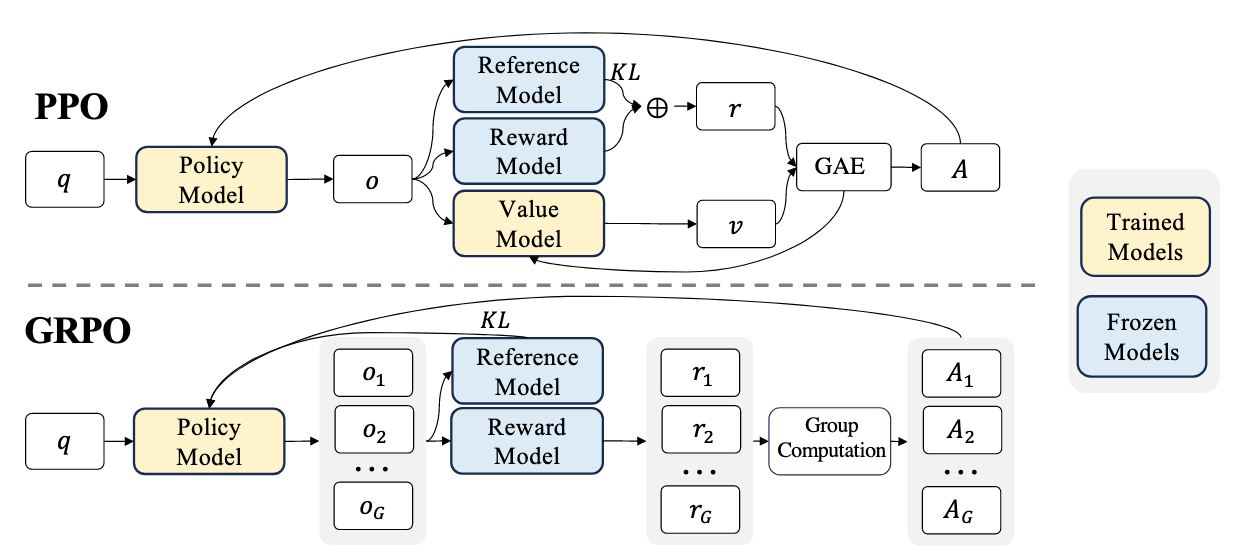
PPO的问题:

• 内存占用大：Value Model 通常和 Policy Model 一样大，显存占用翻倍 。
• 训练困难：在生成任务中，通常只有最后才有 Reward，很难训练一个对每个 Token 都能准确评估的 Value Model

PPO最大化的目标函数: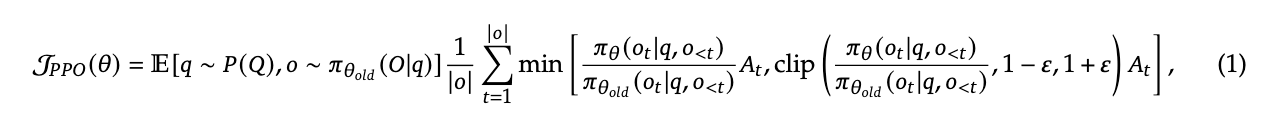

GRPO最大化的目标函数:

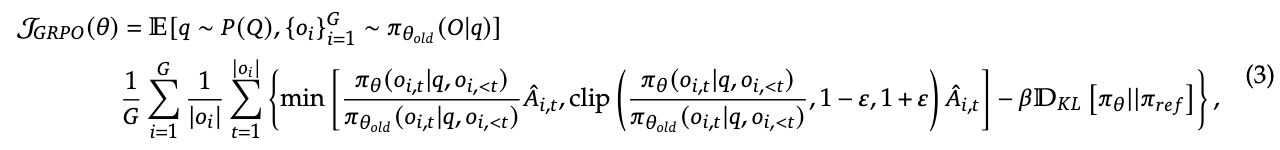
对比:

1. GRPO 没有 Critic 模型。对于同一个问题 $q$，它会从旧策略$\pi_{\theta_{old}}$中采样生成 一组（Group）$G$ 个不同的输出${o_1, o_2, …, o_G}$。
   • 优势$\hat{A}_{i}$的计算是基于这组输出的奖励${r_1, r_2, …, r_G}$进行标准化得来的：
     $$
     \hat{A}_{i} = \frac{r_i - \text{mean}(r)}{\text{std}(r)}
     $$
   • 其中 $\text{mean}(r)$ 是这组输出奖励的平均值，$\text{std}(r)$ 是标准差
2. PPO 通常使用 GAE (Generalized Advantage Estimation) 来平衡偏差和方差，这需要对每一个时间步 $t$ 都有一个价值估计 $V(s_t)$。由于 GRPO 放弃了价值模型，因此无法使用 GAE，而是采用了 Group Computation（组计算）:
   • 对于每一个输出$o_i$, 通过上述公式计算得到$\hat{A}_{i}$, 最后输出为一组 $G$ 个优势值 ${A_1, A_2, …, A_G}$
3. 在PPO的Loss Function中没有包含$(-\beta \mathbb{D}_{KL})$这部分
   • PPO 为什么通常不直接在 Loss 里减 KL？ 在 PPO（以及 RLHF 的标准做法）中，KL 惩罚通常被加在奖励函数 (Reward) 里，即
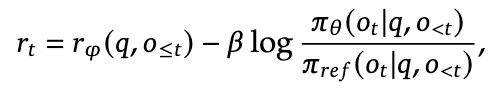
   • GRPO 为什么要直接减 KL？
     
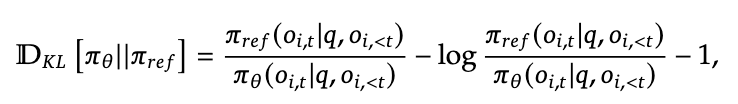
     1. 没有价值函数：GRPO 不需要训练价值函数，所以不需要通过修改 Reward 来“通知”价值函数关于 KL 的惩罚。
     2. 计算稳定性：在 GRPO 中，优势 $\hat{A}$ 是通过 (r - mean) / std 计算的。如果把 KL 惩罚加在 $r$ 里面，那么 KL 项也会被除以 std。这意味着 KL 惩罚的力度会随着组内奖励的方差（std）剧烈波动（方差小惩罚就极大，方差大惩罚就极小），这会导致训练极其不稳定。

GRPO Algorithm:

---

PS.

1. PPO中为什么引入了Importance Sampling
   在数学上，我们希望最大化新策略 $\pi_{\theta}$ 下的期望奖励 $J(\theta) = \mathbb{E}_{\tau \sim \pi_{\theta}}[R(\tau)]$。但我们手里只有从旧策略 $\pi_{\theta_{old}}$ 采样出来的轨迹。
   利用重要性采样，我们可以将期望的计算方式进行转换：

$$
\nabla J(\theta) = \mathbb{E}_{x \sim \pi_{\theta_{old}}} \left[ \frac{\pi_{\theta}(x)}{\pi_{\theta_{old}}(x)} \nabla \log \pi_{\theta}(x) A(x) \right]
$$

2. GRPO的优点

   1. 极致的资源效率：不需要 Critic 模型。这使得你可以用同样的显存训练更大的模型，或者用更大的 Batch Size。
   2. 训练稳定性：通过组内标准化（Normalization），自动适应了不同 prompt 的难度差异，消除了奖励尺度的影响。
   3. 实现简单：省去了 Critic 的网络构建、初始化、前向推理和反向传播代码，流程更清爽。
   4. 无需训练价值函数：规避了“价值估计偏差”的问题，直接利用采样的经验均值。

DeepSeek R1

https://arxiv.org/abs/2501.12948

• DeepSeek-R1-Zero
• DeepSeek-R1
• Distill